La unión de los racionales y los irracionales forma el conjunto de los números reales. 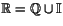 .
.
El conjunto de los reales, con el orden inducido por el orden ya visto en 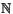 ,
, 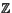 y
y 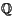 es un conjunto totalmente ordenado.
es un conjunto totalmente ordenado.
Teniendo eso en cuenta, se puede representar gráficamente el conjunto de los reales con una recta, en la que cada punto representa un número.
Muchas de las propiedades que hemos visto para los conjuntos
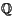
e
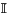
son heredadas por
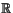
.
Como ya se ha visto, 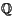 es denso en
es denso en 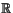 . También
. También 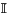 es denso en
es denso en 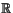 .
.
Podemos considerar 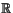 como el conjunto de todos los límites de sucesiones cuyos términos son números racionales.
como el conjunto de todos los límites de sucesiones cuyos términos son números racionales.
A diferencia de lo visto para 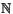 ,
, 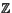 y
y 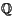 , el conjunto de los reales no es numerable.
, el conjunto de los reales no es numerable.
Los
números reales son los números que se puede escribir con anotación decimal, incluyendo aquellos que necesitan una expansión decimal infinita. El conjunto de los números reales contiene todos los números enteros, positivos y negativos; todos los fracciones; y todos los números irracionales -- aquellos cuyos desarrollos en decimales nunca se repiten. Ejemplos de números irracionales son
√ 2
2 = 1.4142135623730951 . . . π = 3.141592653589793 . . . e = 2.718281828459045 . . .
= 1.4142135623730951 . . . π = 3.141592653589793 . . . e = 2.718281828459045 . . . Es muy útil representar a los números reales como puntos en la
recta real, como mostrado aquí.
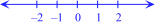
Observe que los números más mayores aparecen a la derecha: Si
a <
b entonces el punto corresponde a
b estrá a la derecha del punto que corresponde a
a.

.
,
y
es un conjunto totalmente ordenado.
es denso en
. También
es denso en
.
como el conjunto de todos los límites de sucesiones cuyos términos son números racionales.
,
y
, el conjunto de los reales no es numerable.
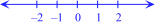

me re sirve esta imfo para el tranajo practico que nos pidio cristina de los numeros reales mui bueno subas mas chicos!! besos
ResponderEliminar